Ansambelsko učenje

Ansambelsko učenje (angleško ensemble learning) je proces v katerem se z načrtnim ustvarjanjem in kombiniranjem različnih osnovnih modelov skuša rešiti problem s področja računske inteligence. Primarno se učenje ansamblov uporablja za povečanje natančnosti napovednih modelov. Priljubljena metafora, ki ponazarja princip delovanja ansambeslkih metod je »glas ljudstva« v kvizu Lepo je biti milijonar.
Oblikovanje ansambla več modelov je običajno bolj učinkovito kot implementacija napovednega modela superiorne zmogljivosti, kadar osnovni modeli v ansamblu zadovoljijo določene pogoje. Pri tem sta bistveni pravilna kombinacija izhodnih podatkov posameznih modelov tako, da se pravilne odločite ojači oz. nepravilne izloči ter raznovrstnost ansambla. Nekatere izmed najbolj pogostih tehnik ustvarjanja ansamblov (bagging in boosting) delujejo na osnovi prerazporejanja učnih podatkov, druge pa se zanašajo na spreminjanje izhodnih podatkov ali selekcioniranja parametrov vhodnih podatkov.
Za oprimalno delovanje ansambelskih metod je pomemben tudi način združevanja napovedi osnovnih modelov. Pri nalogah klasifikacije se za združevanje napovedi najpogosteje uporabljajo različne metode glasovanja, za naloge regresije pa različne oblike povprečenja. Ansambelske metode se uporabljajo tudi za napovedovanje strukturiranih vrednosti.
Ansambelsko učenje se uporablja na številnih področjih, kjer je potrebna ocena zanesljivosti napovedi (npr. finančno odločenje, medicinska diagnostika) ali lahko z združitvijo podatkov iz različnih virov, ki terjajo uporabo različnih osnovnih modelov dosežemo boljšo napovedno natančnost.
Sestavljanje ansambla
[uredi | uredi kodo]Pri oblikovanju ansamblov je potrebno izhode posameznih modelov združi tako, da se pravilne napovedi ojači in napačne zavrže. Pri tem morata biti izpolnjena vsaj naslednja kriterija: natančnost in raznolikost.
Natančen model je tak, ki naredi manj napak kot bi jih naredili z naključnim ugibanjem (pravilno je treba določiti vsaj polovico podatkov).[navedi vir]
Po drugi strani pa bi bilo nesmiselno imeti modele, ki delajo enake napake. Z ustrezno kombinacijo sicer nepopolnih modelov lahko bistveno zmanjšamo končno napako pri napovedih.
Spodnja ilustracija ponazarja ta koncept na primeru klasifikacije podatkovnih točk na podlagi dveh značilk ponazorjenih na x- in y-osi v tri razrede, ki so ponazorjeni s krožci, kvadratki in trikotniki. Vsak model (klasifikator), ki je bil naučen na različnih podmnožicah učnih podatkov (podatki, ki so bili vključeni v posamezno učeno množico so označeni z odebeljeno obrobo) dela različne napake (podatki označeni z rdečo barvo so zunaj območja, ki ga določijo odločitvene meje prikazane s črtkanimi črtami). Kombinacija danih modelov zagotavlja boljšo klasifikacijo kot posamezni modeli (pri skupni odločitveni meji prikazani s polno črto je največ podatkov znotraj pravilnega območja).

Uspeh ansambla si lahko opredelimo kot njegovo zmožnost popravljanja napak posameznih modelov. To je v veliki meri odvisno od raznolikosti modelov, ki sestavljajo ansambel. Večja kot je raznolikost, boljše so možnosti, da bodo slabe odločitve preglasovane.
Zagotavljanje raznolikosti
[uredi | uredi kodo]Da bi zagotovili raznolikost morajo modeli znotraj ansambla delati različne napake na različnih instancah. Raznolikost je možno doseči na več načinov.
Najbolj razširjena metoda je uporaba različnih podatkovnih naborov za učenje posameznih klasifikatorjev. Tovrstni nabori so pogosto pridobljeni s pomočjo tehnik vzorčenja, kot na primer bootstraping ali bagging. Nabori podaktkov za učenje so izrbani naključno iz celotnega nabora podatkov z ali prez ponavljanja.
Poleg tega nastavljanje parametrov učenja omogoča nadziranje (ne)stabilnosti posameznih kalsifikatorjev (stabilnost je definirana kot konsekventnost odločitev klasifikatorja) in tako pripomore k raznolikosti. Šibki klasifikatorji so pogosto uporabljeni kot bazični klaasifikatorji, saj tudi za najmanjše spremembe pri vhodnih podatkih pridejo do drugačnih zaključkov. V ansambel tako lahko združimo po funkcionalnosti sicer popolnoma enakih večplastnih perceptronov, z različnimi začetnimi utežmi, številom plasti, itd.
Alternativen pristop je uporaba popolnoma rezličnih tipov klasifikatorjev, kot na primer kombinacija perceptronov, odločitvneih dreves, metoda podpornih vektorjev.
Podoben efekt ima tudi uporaba različnih značilnosti ali različnih naborov značilnosti. Najbolj znan primer tega pristopa je metoda najklučnih dreves.
Pomembni ansambelski modeli
[uredi | uredi kodo]Učenje ansamblov pa je možno z uporabo različnih strategij, kot so uporaba različnih podmnožic podatkov pri učenju, spreminjanje parametrov osnovnih modelov ali uporaba različnih podmnožic značilk. Sledi pregled nekaterih pomembnejših metod za učenje ansamblov.
Bagging
[uredi | uredi kodo]
Bagging (okrajšava za angl. bootstrap aggregation) je eden najstarejših in najpreprostejših algoritmov za učenje ansamblov, ki ga je leta 1994 predlagal Leo Breiman. Raznolikost klasifikatorjev se doseže z vzorčenjem učnih podatkov po metodi stremena (angl. bootstrap method).
Algoritem: Učenje s pristopom Bagging
Vhod:
primeri – učni podatki
L – osnovni učni algoritem
n – velikost ansambla
f – število ali delež točk v posameznem vzorcu
Za i med 1 in n
vzorec i ← naključni izbor f točk iz množice primeri
model i ← učenje modela s pomočjo L na množici vzorec
Izhod:
Modeli od 1 do n
Končna odločitev ansambla je v primeru klasifikacije razred, izbran s strani večine klasifikatorjev (enostavno glasovanje večine). V primeru verjetnostnih napovedi, napovemo povprečno napovedano verjetnost za vsakega od razredov. Pri regresijskih modelih napovemo srednjo vrednost napovedi posameznih modelov.
Pri metodi bagging se lahko vzorčene množice učnih podatkov znatno prekrivajo, kar lahko vodi do preveč podobnih napovedi med posameznimi modeli v ansamblu.
Naključni gozdovi
[uredi | uredi kodo]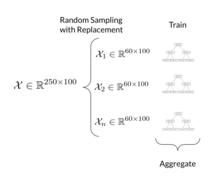
Metodo naključnih gozdov (angl. random forests) lahko opišemo kot različico algoritma bagging, ki za osnovne klasifikatorje uporablja odločitvena drevesa (angl. decision trees). Poleg vzorčenja učnih podatkov, naključni gozdovi za zagotavljanje raznolikosti uporabljajo tudi spremenjen algoritem za učenje odločitvenih dreves.
Osnovna ideja metode naključnih gozdov je dodajanje naključnosti v gradnjo odločitvenih dreves. Namesto izbire najbolj informativne značilke na vsakem nivoju drevesa, je Brieman predlagal naključno izbiro značilke izmed najbolje ocenjenimi značilkami, kjer je privzeto nastavljen na koren števila primerov v učni množici (zaokroženo navzdol; ). Na ta način se zagotovi različnost odločitevnih dreves v naključnem gozdu.
Pri napovedovanju s pomočjo naključnega gozda, se v posameznih odločitvenih drevesih vhodni podatek (značilke, ki opisujejo podatek) vnese na vrhu. Med spuščanjem po drevesu (glede na vrednosti značilk) je nabor možnih odgovorov vedno manjši, dokler ni mogoče določiti končne napovedi.
Pri metodi naključnih gozdov je glavni parameter število dreves v gozdu, tipično se uporablja nekaj sto dreves. Naključni gozdovi veljajo za metodo z visoko napovedno natančnostjo, kratkim napovednim časom ter se lahko uporabijo tudi za probleme z neuravnoteženimi učnimi množicami (bistveno različno število primerov za različne napovedi) oz. manjkajočimi podatki. Slabosti naključnih gozdov so, da pri uporabi za regresijo ne morejo napovedati zunaj obsega v učnih podatkih ter da so občutljivi na prekomerno prileganje (angl. overfitting) v primeru podatkov z veliko šuma.
Osnovni algoritem je leta 1995 predlagal Tin Kam Ho.[1] Kasneje sta ga razširila Breiman[2] in Cutler[3] ter prijavila blagovno znamko.[a]
Boosting
[uredi | uredi kodo]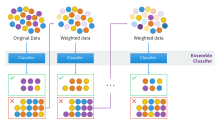
Boosting (angl. za krepitev) je meta-algoritem, ki naslavlja vprašanje, ali lahko več šibkih modelov tvori močnega, ki ga je leta 1988 postavil Michael Kearns,[4] rešitev pa je dve leti kasneje predlagal Robert Schapire.[5]
Podobno kot pri baggingu se tudi pri boostingu s ponovnim vzorčenjem podatkov ustvari ansambel klasifikatorjev, ki se jih združi z glasovanjem. Vendar pa je pri boostingu vzorčenje nastavljeno tako, da izbira najbolj informativne učne primere za vsak naslednji klasifikator. Ponavadi se to izvede s povečanjem uteži tistih primerov, ki jih je prejšnji model napovedal nepravilno. Na ta način boosting zagotavlja preprosto in učinkovito metodo za spreminjanje šibkih modelov v močne modele.
Za prvo praktično implementacijo velja algoritem AdaBoost (okrajšava za adaptivno krepitev, oz. angl. adaptive boosing), ki sta ga leta 1996 predlagala Yoav Freund in Robert Schapire[6]. Njegova objava je bila odmevna in je v strojnem učenju v 90. letih povzročila pomik od raziskav optimizacije posameznih metod k ansamblskim metodam. Algoritem je pomembno vplival tudi na razvoj drugih krepitvenih metod, ki so ga sčasoma presegle.[7]
Zlaganje
[uredi | uredi kodo]Pri zlaganju (angl. stacking, tudi stacked generalization) so izhodi posameznih modelov v ansamblu vhodi za drug model strojnega učenja. Na podlagi izhodov se ta model nauči napovedovati končni rezultat. Učenje je dvostopenjsko. Najprej se nauči osnovne modele z uporabo razpoložljivih podatkov, nato se nauči ločen model združevalca za izdelavo končne napovedi z uporabo vseh napovedi osnovnih modelov.
Združevanje praviloma daje boljše rezultate kot katerikoli od posameznih naučenih modelov.[8] Uspešno je bil uporabljen tako za različne naloge nadzorovanega kot nenadzorovanega učenja.
Naivni Bayesov klasifikator
[uredi | uredi kodo]Ta članek potrebuje razširitev. Pomagajte Wikipediji in ga razširite. Pri tem si pomagajte z informacijami na njegovi pogovorni strani. (mesec ni naveden ) |
Pristopi za združevanje napovedi
[uredi | uredi kodo]Za združevanje napovedi se pri ansambelskih metodah uporabljajo različni pristopi. Nekateri pristopi delujejo izključno na podlagi napovedih posameznih osnovnih modelov (npr. prvi in drugi model napovesta razred A, tretji napove razred B, četrti spet razred A), medtem ko drugi uporabljajo tudi druge podatke (npr. s kakšno verjetnostjo je nek osnovni model napovedal različne možnosti oz. njihovo razvrstitev)[9] ali pa ločen model za določitev končne napovedi (kot pri zlaganju)[10].
Pri nalogah klasifikacije se za združevanje napovedi najpogosteje uporabljajo različne metode glasovanja, za naloge regresije pa različne oblike povprečenja napovedi.
Klasifikacija
[uredi | uredi kodo]Najpogosteje se uporablja večinsko glasovanje (angl. majority voting, tudi plurality voting).
S kjer je število osnovnih modelov in število možnih izhodov, označimo odločitve posameznih modelov v ansamblu. Če -ti model v ansamblu izbere razred potem je sicer 0.
Uteženo oz. ponderirano večinsko glasovanje deluje podobno:
Uteževanje modelov ima v primerjavi z običajnim večinskim glasovanjem prednost, da lahko tvori modele z večjo natančnostjo pri končni napovedi.
Tovrstno glasovanje ne uporabi vseh razpoložljivih podatkov, ki jih lahko pridobimo iz posameznih modelov v ansamblu. S pomočjo različnih algebraičnih izrazov, kot so minimum, maksimum, vsota, povprečje, produkt, mediana itd.[10] lahko uporabimo tudi zvezne podatke (npr. verjetnost posamezne napovedi). Končna odločitev ansambla je razred , ki dobi največjo podporo , potem ko se algebraični izraz uporabi za posamezne možne napovedi za vhod z značilkami :
- povprečenje: ,
- (utežena) vsota: , kjer so uteži dodeljene glede na neko merilo
- izračun produkta:
- izračun maksimuma:
- izračun minimuma:
- izračun mediane:
Problem algebraičnih metod je, da jih ni mogoče učiti niti prilagajati. Zato se včasih uporabijo bolj zapleteni izrazi, ki se bolje prilegajo danemu problemu.[10]
Ko imamo opravka z večdimenzionalnimi izhodi se lahko uporablja tako imenovane odločitvene predloge [11]. Te izračunajo metriko podobnosti (npr. kvadrat evklidske razdalje) med odločitvenim profilom (napovedi posameznih modelov v ansamblu) za primer, ki ga je treba razvrstiti ter povprečnim odločitvenim profilom za znane primere vsakega razreda posebej.
Kratek pregled načinov združevanja napovedi je podan v tabeli.
| Pristop | Komentarji |
|---|---|
| preprosto večinsko glasovanje | predpostavlja neodvisne osnovne modele |
| pondirano glasovanje | za dosego optimalnih rezultatov morajo biti uteži sorazmerne s točnostjo posameznega modela |
| vsota, povprečje, mediana | robusten pristop, ki predpostavlja neodvisne ocene zaupanja |
| produkt, min, max | zahteva med seboj nepovezane značilke, občutljiv za osamelce |
| odločitvene predloge | primeren za večdimenzionalne izhode |
Razlogi za uporabo ansambelskih metod
[uredi | uredi kodo]Optimizacija količine učnih podatkov
[uredi | uredi kodo]Učenje ansamblov je praktično tako v primeru spopadanja s preveliko količino podatkov kot kadar jih primanjkuje.
Če imamo preveč podatkov, da bi bilo učenje enega klasifkatorja učinkovito jih je smiselno porazdeliti v manjše nabore in opraviti učenja na vsakem klasifikatorju ločeno. V situacijah s premalo podatki pa se lahko uporablja večkratno vzorčenje tako da se uči različne klasifikatorje, ki vsak uporabljajo svoj vzorec. Vzorci so naključno izbrani iz originalnega nabora podatkov s ponovitvami.
V obeh primerih se tako nastale klasifikatorje združi v ansambel, ki da končni odgovor.
Združevanje podatkov iz raznovrstnih virov
[uredi | uredi kodo]V številnih primerih ponujajo podatki pridobljeni iz različnih virov komplementarne informacije. Združevanje informacij lahko vodi k boljši natančnosti odločitev klasifikacije kot če bi bile odločitve bazirane zgolj na posameznih virih informacij.[10]
Ansambelske metode se pogosto uporabljajo na področjih, kjer lahko z združitvijo podatkov iz različnih virov, ki terjajo uporabo različnih modelov, izboljšamo napovedi. Pri diagnostiki nevroloških težav se lahko na primer uporabi podatke pridobljene iz elektroencefalograma, magnetne resonance, ali positronskoemisijske tomografije skupaj z demografskimi podatki pacienta. Taka množica podatkov vključuje raznovrstne lastnosti, ki ne morejo biti istočasno uporabljeni za učenje enega samega klasifikatorja. V ta namen se uporablja ansamble klasifikatorjev, ki so posamično prilagojeni za učenje na podlagi različnih tipov vhodnih podatkov.
Reševanje kompleksih problemov klasifikacije
[uredi | uredi kodo]
Včasih je klasifikacija pretežka naloga za en sam klasifikator. Odločitvena meja, ki loči podatke med različne razrede je lahko prezapletena, da bi jo bilo možno predstaviti z izbranim modelom.
Tako so linearni klasifikatorji denimo zmožni zgolj učenja linearnih ločitvenih meja, vendar pa lahko primerno kombinacijo le teh naučimo poljubnega nelinearnega razločitvenega vzorca. Dvorazrednega klasifikacijskega problema na sliki ni možno rešiti z uporabo zgolj enega linearnega kasifikatorja. Kljub temu pa lahko s kombinacijo treh klasifikatorjev, ki klasificirajo pozitivno na eni in negativno na drugi strani, sestavimo tikotni klasifikator, ki definira področje, ki ga sicer ne bi bilo mogoče izraziti.
V tem pogledu učenje ansamblov sledi princpu metode deli in vladaj, tako da razdeli podatkovni prostor v manjše in lažje naučljive razdelke, kjer se vsak izmed klasifikatorjev nauči razločevati zgolj enostavne probleme. S primerno kombinacijo različnih klasifikatorjev se sestavi kompleksnejši vzorec odločitvene meje.[10]
Ocena stopnje zaupanja v statistiki
[uredi | uredi kodo]Ansambelske metode se uporabljajo tudi v statistiki za kvantitativno oceno zaupanja odločitev. Če se velika večina modelov v ansamblu strinja z odločitvijo za določen primer problema, lahko to razlagamo kot odločitev z visoko stopnjo zaupanja. Po drugi strani pa, ima končna odločitev majhno stopnjo zaupanja, kadar modeli predlagajo različne rešitve.
Inkrementalno učenje
[uredi | uredi kodo]Na področju umetne inteligence se neredko srečujemo z dinamičnimi okolji, kjer se sčasoma pojavljajo novi podatki ali novi razredi podatkov (npr. spremenjena zakonodaja uvede nov prometni znak, ki ga mora razpoznati sistem za prepoznavanje znakov). Postopno učenje se nanaša na sposobnost algoritma, da se uči iz novih podatkov, ki so lahko na voljo po tem, ko je bil klasifikator že naučen iz predhodno razpoložljivega nabora podatkov. Proces učenja poteka, kadar koli se pojavijo novi primeri, in prilagaja naučeno glede na nove primere. Namesto da bi bilo treba vsakič, ko dobimo nove podatke, ponoviti celoten proces učenja modelov, se lahko uporabijo ansambelski sistemi, npr. z vključitvijo dodatnega klasifikatorja, ki lahko operira z novimi podatki.[13]
Implementacije v programskih okoljih
[uredi | uredi kodo]- R: na arhivu paketov CRAN obstaja več različnih paketov, ki implementirajo glavne ansambelske metode.[14]
- Python: knjižnica scikit-learn za strojno učenje vključuje paket za ansambelsko učenje z implementacijami pomembnejših ansambelsih metod.[15]
- MATLAB: ansambelske metode so vključene v razširitvi za statistiko in strojno učenje (angl. Statistics and Machine Learning Toolbox).[16]
Glej tudi
[uredi | uredi kodo]Sklici
[uredi | uredi kodo]- Opombe
- ↑ Blagovna znamka je bila 19. decembra 2006 v ZDA registrirana pod prijavno številko 3185828.
- Viri
- ↑ Ho, Tin Kam (1995). Random Decision Forests (PDF). Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, 14–16 August 1995. str. 278–282. Arhivirano iz prvotnega spletišča (PDF) dne 17. aprila 2016. Pridobljeno 5. junija 2016.
- ↑ Breiman, Leo (2001). »Random Forests«. Machine Learning. 45 (1): 5–32. doi:10.1023/A:1010933404324.
- ↑ Liaw, Andy (16. oktober 2012). »Documentation for R package randomForest« (PDF). Pridobljeno 15. marca 2013.
- ↑ Michael Kearns (1988). »Thoughts on hypothesis boosting« (PDF). Pridobljeno 24. februarja 2024.
- ↑ R.E. Schapire (1990). »The strength of weak learnability«. Machine Learning. 5: 197–227. doi:10.1007/BF00116037.
- ↑ Yoav Freund; Robert E Schapire (1996). »Experiments with a new boosting algorithm«. Proceedings of the International Conference on Machine Learning (ICML). Zv. 96. str. 148–156.
- ↑ A. Mayr, H. Binder, Olaf Gefeller, M. Schmid (2014). »The Evolution of Boosting Algorithms«. Methods of Information in Medicine. 53: 419–427. doi:10.3414/ME13-01-0122.
{{navedi časopis}}: Vzdrževanje CS1: več imen: seznam avtorjev (povezava) - ↑ Wolpert (1992). »Stacked Generalization«. Neural Networks (v angleščini). 5 (2): 241–259. doi:10.1016/s0893-6080(05)80023-1.
- ↑ Liying Xu; Adam Krzyżak; Ching Yee Suen (1992). »Methods for combining multiple classifiers and their applications to handwriting recognition«. IEEE Transactions on Systems, Man, and Cybernetics. 22 (3): 418–435.
- ↑ 10,0 10,1 10,2 10,3 10,4 Polikar, Robi (2006). »Ensemble based systems in decision making«. Circuits and Systems Magazine, IEEE (6.3).
- ↑ Ludmila I. Kuncheva; James C. Bezdek; Robert P.W. Duin (2001). »Decision templates for multiple classifier fusion: an experimental comparison«. Pattern Recognition. 34 (2): 299–314. doi:10.1016/S0031-3203(99)00223-X. ISSN 0031-3203.
- ↑ Martin Sewell (2008). »Ensemble learning« (PDF). Pridobljeno 24. februarja 2024.
- ↑ Michael D Muhlbaier and Robi Polikar. An ensemble approach for incremental learning in nonstationary environments. In Multiple classifier systems, pages 490--500. Springer, 2007.
- ↑ »The Comprehensive R Archive Network«. Pridobljeno 24. februarja 2024.
- ↑ »Ensembles: Gradient boosting, random forests, bagging, voting, stacking«. Pridobljeno 24. februarja 2024.
- ↑ »Classification Ensembles«. MATLAB & Simulink. Pridobljeno 8. junija 2017.




















